[Deep Learning Specialization] C1-W3: One Hidden Layer Neural Network

이 기록은 내가 학기 중에 수강했던 Coursera의 'Deep learning specialization' 강의를 다시 복습하는 용도이다. 이미 2번 정도 학습을 마친 상태이고, 내 기준 헷갈리거나 메모하면 좋을 핵심 내용 위주로만 작성했다. 즉, 처음 수강하는 사람들에겐 내 복습 기록들이 도움이 되진 않을 수 있다. 그런 사람들에겐 직접 수강하고 자신만의 복습 노트를 만드는 것을 추천한다.

 

Neural Networks Overview

Neural Network Representation

• Neural Network는 Input layer, Hidden layer, 그리고 Output layer로 이루어져 있다.
  • 이건 two layer로 이루어진 NN이다. (input layer는 고려하지 않음)

Computing a Neural Network's Output

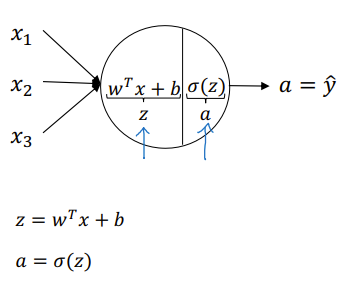
• After computation of the linear formula, put it into activation function
• Vectorization for one single training example:

• Vectorizing across multiple examples:

Activation Functions

• Introducing non-linearity
  • Why do we need non-linear activation functions?
    • 만약 activation function이 linear이라면 layer가 몇개 있어도 결국 최종 식은 linear임. 즉, 복잡한 계산을 못하게 되어 복잡한 feature 추출이 불가능하게 됨.

 

Random Initialization

• to avoid symmetry issues and facilitate effective learning
  • Symmetry Issue:
    • 만약 Network의 모든 weights를 0으로 initialization하면, 모든 neuron들이 동일한 입력을 받고 동일한 출력을 생성하게 됨.
      • 즉, neuron들이 서로 구별되지 않고 동일하게 학습됨.
    • Weights가 모두 0일 때, 각 weight에 대한 gradient도 동일하게 계산됨.
      • 이는 뉴런들이 같은 방향으로 업데이트된다는 것을 의미함. 따라서, weight가 초기화된 값에서 벗어나지 못하고 학습이 제대로 이루어지지 않음.
  • Weights를 무작위로 초기화하면, neuron들이 서로 다른 입력을 받아 서로 다른 출력을 생성하게 됨. 이는 neuron들이 독립적으로 학습할 수 있게 하여, 대칭성 문제를 해결할 수 있음.
    • We prefer very small number for random initialization
      • 크게 잡게 되면 Gradient가 작아져 속도가 느려짐. (Random Initilization Figure 참)

Weight를 0으로 initialization 했을 경우

Random Initilization